问题
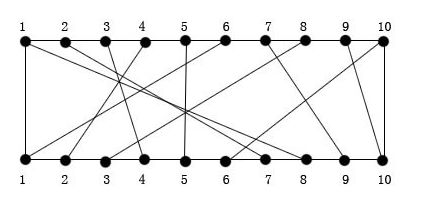
在一块线路板的前后两边各自有n个接线头。依据电源电路设计方案,规定用输电线 (i,π(i)),将上方接线头 i 与下方接线头 π(i) 相接,
如下图,在其中 π(i),1《=i《=n,是(1,2……,n)的一个排序。输电线(i,π(i))称之为该电路板上的第i条连线。针对一切 1《=i《s《=n,第i条连线和第s条连线相交的充分且必要条件是 π(i) 》 π(s)。
ps:留意 π(pi) 和 n,并不是小写字母的n,别看错
问:在制做线路板时,规定将这n根线遍布到多个电缆护套上,在同一层上的连线不可以交点。电源电路走线问题要明确将什么连线分配在第一层上,促使该层上面有尽量多的连线。
详细描述
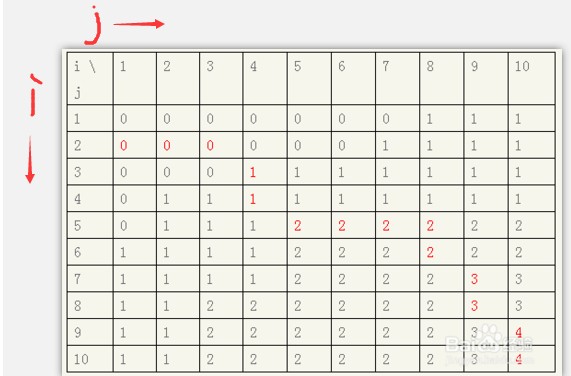
最先 左右都各有 n 个接线头,用 a[i] 二维数组表明 与 上接线头 相接线的 下接线头,再用 set[i][j] 表明上接线头 i 与下接线头 j 相接线的 左侧(包含 i ,j 连线)的最高不交点连线的数量。
ps(这儿的 j ,i 和上边问题上说的并不是一个物品,这儿的 i指的是上接线头,j指的是下接线头)
1、公式计算如下所示:
假如 j != a[i] 则 max( set[i-1][j],set[i][j-1] )
set[i,j] =
假如 j == a[i] 则 set[i-1][j-1] 1
循环系统解析xml i 和 j ,实际应用 i X j 的嵌套循环,实际上便是每一个上接线头和每一个下接线头做一次配对,那样就可以得到結果,set[n][n]即大家需要的結果。最终根据回朔把数据导出出去
==》 j == a[i],表明当图中中的某一左右接线头相接时,这时这两个点不容易在和别的的接线头相接,
这时在 (i ,j) 处的最高不交点连线的数量就应该是便是 第 i-1个上接线头 和第 j-1个下接线头时的 较大不交点连线的数量 1。这一 1很重要。
==》 j != a[i],表明当图中中的某一左右接线头相接时,这时 i 点和 非 j 点相接, j 点和 非 i 点相接,
这时在( i ,j) 处的最高不交点连线的数量就应当和 ( i – 1,j ) 处较大不交点连线的数量、 ( i,j – 1)处较大不交点连线的数量中比较大的最高不交点连线的数量同样。
2、参照图如下所示:
鲜红色标出的便是优化算法采用的途径(往上优先选择,还可以用往左边优先选择,回答全是四个,但值会出现一点不一样)。在倾斜角值更改时可以获得所愿的非空子集。即 9-》10,7-》9, 5-》5, 3-》4
代码块
#include 《stdio.h》
#include 《stdlib.h》
#define MAX( a, b ) ( (a) 》 (b) ? (a) : (b) )
void circut( int a[], int set[][11], int n );
void back_track( int i, int j, int set[][11] );
int main()
{
int a[] = { 0, 8, 7, 4, 2, 5, 1, 9, 3, 10, 6 };
int set[11][11];
circut( a, set, 10 );
printf( “max set: %d \\n”, set[10][10] );
back_track( 10, 10, set );
printf( “\\n” );
system( “pause” );
return(0);
}
void circut( int a[], int set[][11], int n )
{
int i, j;
for ( i = 0; i 《 n; i )
{
set[i][0] = 0;
set[0][i] = 0;
}
for ( i = 1; i 《= n; i )
{
for ( j = 1; j 《= n; j )
{
if ( a[i] != j )
set[i][j] = MAX( set[i – 1][j], set[i][j – 1] );
else
set[i][j] = set[i – 1][j – 1] 1;
}
}
}
void back_track( int i, int j, int set[][11] )
{
if ( i == 0 )
return;
if ( set[i][j] == set[i – 1][j] )
back_track( i – 1, j, set );
else if ( set[i][j] == set[i][j – 1] )
back_track( i, j – 1, set );
else{
back_track( i – 1, j – 1, set );
printf( “(%d,%d) ”, i, j );
}
}
算法复杂度
circut 的算法复杂度为O(n2)
back_track的算法复杂度为 O(n)
若有不正确请纠正。
该文章内容提高散播新技术应用新闻资讯,很有可能有转截/引入之状况,若有侵权行为请联络删掉。
上一篇: 电路板受潮会引发哪些问题?
下一篇: 基于新故障模型的测试方案的研究分析
 派旗纳米·官方网站
派旗纳米·官方网站
