《算法设计与分析》 –王晓东
题型叙述:
在一块线路板的上、下2端各自有n个接线头。依据电源电路设计方案,规定用输电线(i,a(i))将上方接线头与下方接线头相接,在其中a(i)表明上节点i相匹配的向节点的值。如下图所示:
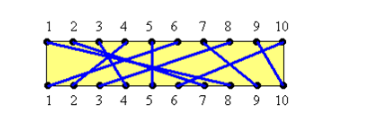
题型规定是在给出的连线中,选择不交点连线的较大非空子集,即不交点连线的较大数额。并把较大不交点非空子集的状况给例举解决啊。
解题思路:
最先用a[i]二维数组表明与上边对应的点相接线的下边的点,再用set[i][j]表明上边连接点i与下边连接点j连线的左侧(包含i j连线)的最高不交点连线的数量。
因此就会有公式计算:
max(set[i-1][j], set[i][j-1]); j != a[i]
set(i,j) =
set[i-1][j-1] 1; j == a[i]
随后就可以对每一个i,都对因此的j求一遍。那样就可以得到結果吗,set[n][n]即大家需要的結果。
最终根据回朔把数据导出出去。
编码完成:
#include 《stdio.h》
#define MAX(a,b) ((a) 》 (b) ? (a) : (b))
void circut(int a[],int set[][11],int n);
void back_track(int i,int j,int set[][11]);
int main()
{
int a[] = {0,8,7,4,2,5,1,9,3,10,6};
int set[11][11];
circut(a,set,10);
printf(“max set: %d \\n”,set[10][10]);
back_track(10,10,set);
printf(“\\n”);
return 0;
}
void circut(int a[],int set[][11],int n)
{
int i,j;
for (i = 0; i 《 n; i )
{
set[i][0] = 0;
set[0][i] = 0;
}
for (i = 1; i 《= n; i )
{
for (j = 1; j 《= n; j )
{
if (a[i] != j)
set[i][j] = MAX(set[i-1][j],set[i][j-1]);
else
set[i][j] = set[i-1][j-1] 1;
}
}
}
void back_track(int i,int j,int set[][11])
{
if (i == 0)
return;
if (set[i][j] == set[i-1][j])
back_track(i-1,j,set);
else if (set[i][j] == set[i][j-1])
back_track(i,j-1,set);
else
{
back_track(i-1,j-1,set);
printf(“(%d,%d) ”,i,j);
}
}
该文章内容提高散播新技术应用新闻资讯,很有可能有转截/引入之状况,若有侵权行为请联络删掉。
上一篇: 案例分析:电路布线问题
下一篇: PCB板常见缺陷分析之电路板常见焊接缺陷
 派旗纳米·官方网站
派旗纳米·官方网站
