简述：电路板电路布线的设计

问题描述：

在一块线路板的上、下两边各自有n个接线头。依据电源电路设计方案，规定用输电线（i，π（i）） 将上方接线头i与下方接线头π（i）相接，如下图。在其中，π（i），1≤ i ≤n，是｛1，2，…，n｝的一个排序。输电线（I， π（i））称之为该电路板上的第i条连线。针对一切1 ≤ i ≤ j ≤n，第i条连线和第j条连线交点的充要条件是π（i）》 π（j）。

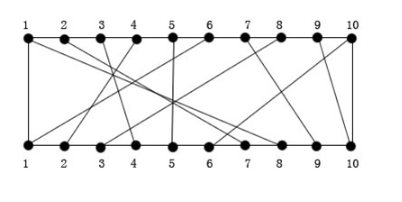
π（i）=｛8，7，4，2，5，1，9，3，10，6｝

在制做线路板时，规定将这n条连线遍布到多个电缆护套上。在同一层上的连线不交点。电源电路走线问题要明确将什么连线分配在第一层上，促使该层上面有尽量多的连线。也就是说，该问题规定明确输电线集Nets = ｛i，π（i），1 ≤ i ≤ n｝的更大的一个非空子集，这一子集中化的输电线相互之间不交点。

问题分析：

显而易见这是一个组成问题，针对组成问题怎求最优解的方式基本上全是动态规划算法。如今描述一下怎样区划子问题：

用B（i，j）表明最优解，在其中，i是上方接线头的编号，j是下方接线头的编号，B（i，j）表明编号小于或等于i的上方接线头和编号小于或等于j的下方接线头中不交点连线的较大结合。 用size（i，j）表明结合中输电线的数额（size（i，j）=|B（i，j）|）。B（i，j）的值含有在B（i-1，j）和B（i，j-1）这俩身高问题中，针对有2xN个接线头的线路板，那麼B（N，N）便是其解了。

针对上方接线头t，用 π（t）表明与他相接的下方接线头

那麼递推公式为：

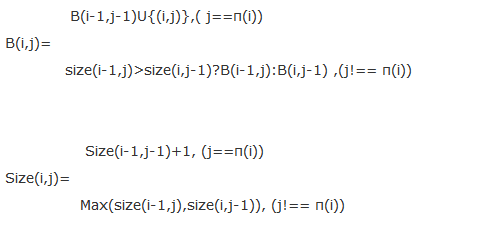
递推公式证实：

针对从B（i-1，j）或B（i，j-1）到B（i，j）要不会加多一条输电线，要不不用。

1. 当 j==π（i）时，（i，j）则是一条输电线，且这一条输电线对B（i-1，j-1）的值沒有危害，由于B（i-1，j-1）中的随意的一条输电线的连接点编号（不论是上方连接点编号或是下方连接点编号）都低于i，j，这由其室内空间部位决策的。

如今求B（i，j）， 即求编号小于或等于i的上方接线头和编号小于或等于j的下方接线头中不交点输电线的较大结合。显而易见该是B（i-1，j-1）U（i，j）。

2 。 当j！= π（i）时。倘若问题是以B（i，j-1）到B（i，j），那麼下方新进入的接线头j要不与上端1至i-1个接线头组成输电线（与第i个接线头组成输电线的状况在上面早已探讨），要不不组成。

假如组成得话那麼这样的事情实际上早已在B（i-1，j）中探讨了，这儿不考虑到。那麼B（i，j） 该是编号区段比他小一点的子问题的解。小一点多少钱，毫无疑问便是少一个接线头了，也就是B（i-1，j）。

如果不组成得话，那麼B（i，j）毫无疑问便是编号区段比他小一点的子问题的解了。

针对B（i，j）很有可能由B（i-1，j）或B（i，j-1）衔接而成，因此B（i，j）取在其中比较大的一个。

该文章内容提高散播新技术应用新闻资讯，很有可能有转截/引入之状况，若有侵权行为请联络删掉。